∆ Definition 1. Pascal's triangle is a triangular array of numbers such that the $n$-th line consists of $n$ numbers, where each number is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as $0$. The number that is on the $(k+1)$-th place of the $(n+1)$-th line is denoted by $\binom{n}{k}$.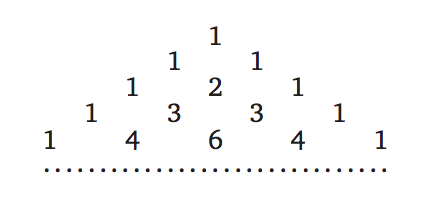

Problem 1. Write down the fist eleven lines of Pascal's triangle. Send a solution

Problem 2. Show that $\binom{n}{k}=\binom{n}{n-k}$. Send a solution

Problem 3. Suppose we want to pass from the bottom left corner of the $m\times n$ rectangle to the upper right corner, by walking eighr up or right. Show that the number of ways to do that is $\binom{n+m}{m}$. Send a solution

Problem 4. * In which lines of Pascal's triangle are all the numbers odd? Send a solution

∆ Definition 2. An $m$-combination from $n$ elements is a subset of $m$ elements from $n$ given elements. The number of $m$-combinations from $n$ elements is denoted by $C_n^m$.

Problem 5. Compute the following 1) $C_{100}^1$, 2) $C_4^2$, 3) $C_5^2$, 4) $C_6^4$. Send a solution

Problem 6. Show that 1) $C_n^k=C_n^{n-k}$ 2) $C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$. Send a solution

Problem 7. Show that $\binom{n}{k}=C_n^k$. Send a solution

Problem 8. Open the parentheses and simplify the following expressions 1) $(a+b)^3$ 2) $(a+b)^4$ 3) $(2a+3b)^4$. Send a solution

Problem 9. (Binomial expansion) 1) Open the parentheses in the following expressions $(a+b)$, $(a+b)^2$, $(a+b)^3$, $(a+b)^4$ and write down the results one under the other. Note that the coefficients form Pascal's triangle. 2) Show that \begin{equation*} (a+b)^n = \binom{n}{0}a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b^2 + ... + \binom{n}{n}b^n. \end{equation*}. Send a solution

Problem 10. Show that 1) $\binom{n}{0}+\binom{n}{1}+...+\binom{n}{n}=2^n;$ 2) $\binom{n}{0}-\binom{n}{1}+...+(-1)^n\binom{n}{n}=0$. Send a solution

Problem 11. Show that $\binom{n}{k}=\frac{n!}{k!(n-k)!}$. Send a solution

Problem 12. Show that \begin{equation*} \begin{array}{ll} 1) \binom{n}{0}^2+\binom{n}{1}^2+...+\binom{n}{n}^2=\binom{2n}{n};\\ 2) \binom{n}{0}+\binom{n+1}{1}+...+\binom{n+k-1}{k-1}+\binom{n+k}{k} = \binom{n+k+1}{k}; \\ 3) \binom{n}{1}+2\binom{n}{2}+...+n\binom{n}{n}= n2^{n-1};\\ 4) \binom{n}{k}\cdot\binom{n-k}{m-k}=\binom{m}{k}\cdot\binom{n}{m}. \end{array} \end{equation*} Send a solution

Problem 13. Let $A$ be a set with $16$ elements. What number is larger: the number of subsets of $A$ consisting of at least 9 elements, or the number of subsets of $A$ consisting of at most 7 elements, or the number of subsets of $A$ consisting of exactly 8 elements? Send a solution

Problem 14. Find the number of sequences of length 16 consisting of zeros and ones such that there are at least three ones. Send a solution

Problem 15. * In how many ways can non-negative numbers $x_1,x_2,...,x_m$ be chosen such that $x_1+x_2+...+x_m=n$? Send a solution