∆ Definition 1. A graph is a pair $\Gamma=(V, E)$, where $V$ is a finite set of vertices and $E$ is a set of edges that consisnts of unordered pairs of vertices.

∆ Definition 2. Two graphs $\Gamma_1$ and $\Gamma_2$ are called isomorphic if there is a bijection $f\colon V(\Gamma_1)\to V(\Gamma_2)$ such that vertices $A$ and $B$ of graph $\Gamma_1$ are connected with an edge if and only if vertices $f(A)$ and $f(B)$ are connected by an edge in $\Gamma_2$.

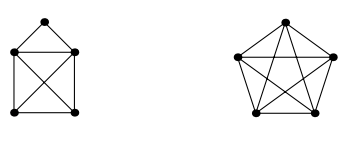
Problem 1. Which of the following graphs are isomorphic? Send a solution

Problem 2. Draw all possible non-isomorphic graphs with at most four vertices. Send a solution

Problem 3. 1) Draw a graph with vertices that are countries in South America, and connect the vertices if countries have a common border. 2) Draw a graph with vertices that are integers between 1 and 15, and connect the vertices if one number is divisible by the other. Send a solution

Problem 4. 1) Draw a graph with five vertices such that it has neither three pairwise connected vertices nor three pairwise disconnected vertices. 2) Show that in any group of six people we can find either three pairwise acquainted people or three pairwise unacquainted people. Send a solution

Problem 5. Suppose in a group of people among any three of them there are at least two friends. Can we split this group into two in such a way that any two people from one group are friends? Send a solution

Problem 6. Find the maximum possible number of edges in a graph with $n$ vertices if 1) among any three 2*) among any four of its vertices there are two that are not connected by an edge. Send a solution

∆ Definition 3. The degree of a vertex $A$ is the number of edges that are incident to it. Notation: $\deg A$.

Problem 7. Give the degrees of all the vertices of the graphs from Problem 1, 2, 3. Send a solution

Problem 8. Show that in a graph with at least two vertes there are two vertices with the same degree. Send a solution

Problem 9. Show that the sum of degrees of any graph is equal to the doubled number of its vertices. Send a solution

∆ Definition 4. A path is a finite sequence of vertices (not necessarily distinct) such that any two consequent vertices are connected by an edge. A path is passing through an edge if the edge connects a pair of consequent vertices of the path. A cycle is a path such that its first and its last vertex is the same. The length of a path is the number of the edges that the path is passing. On this page, we consider only graphs without parallel edges (two or more edges that are incident to the same two vertices). A path can be uniquely determined by the sequence of its vertices, but sometimes it is handy to include edges into the notation.

∆ Definition 5. A Hamiltonian graph is a graph with a path that contains each vertex exactly once.

Problem 10. Show that a graph of a dodecahedron and a graph of an icosahedron are Hamiltonian graphs. Send a solution

∆ Definition 6. A graph is called connected if for any of its vertices there is a path that starts at one vertex and ends at the other.

Problem 11. Which graphs from Problem 1, 2, 3 are connected? Send a solution

Problem 12. Show that if a graph with at least two vertices is connected, then the degree of any vertex is positive. Is the inverse true? Send a solution

∆ Definition 7. A connected graph is called a tree if it contains no cycles.

Problem 13. Show that any tree has a vertex with degree one. Send a solution

Problem 14. Show that in a tree, the number of vertices is bigger than the number of edges by one. Send a solution

Problem 15. Below you see a map of bridges in the eighteen century Königsberg. Can a pedestrian walk in such a way that she passes each bridge exactly once? 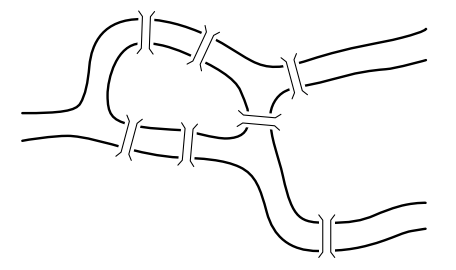Send a solution

∆ Definition 8. A graph is called Euler graph is it contains a cycle that passes each edge exactly once.

Problem 16. Show that the following graphs are Euler graphs. Send a solution

Problem 17. Show that a graph is Euler if and only if it is connected and the degree of each vertex is even. Send a solution

Problem 18. * There are $n$ teams in a competition. Each team played with each other team once and there were no ties in the competition. Show that the teams can be numbered $1,...,n$ in such a way that $(i+1)$-th team beats $i$-th, for any $i=1,...,n-1$. Send a solution

Problem 19. * (Ramsey's theorem) 1) Show that for any natural (non-negative integer) numbers $m,n$ there is a natural number $k$ such that in any graph with $k$ vertices there are either $m$ pairwise connected vertices or $n$ pairwise disconnected. The smallest $k$ is denoted by $R(m,n)$. 2) Find $R(3,4)$. Send a solution

∆ Definition 9. The distance between vertices is the length of the shortest path that connects them. The diameter of a graph is the longest distance between its vertices.

∆ Definition 10. A graph is called regular with valency $k$ if the degree of each of its vertex is equial to $k$.

∆ Definition 11. Moore graph is a regular graph with valency $k$ with number of vertices $k^2+1$ and diameter at most $2$.

Problem 20. *1) Show that a regular graph with valency $k$ and diameter $2$ cannot have more than $k^2+1$ vertices. 2) Give examples of Moore graph for $k=1,2,3$. 3) Is there a Moore graph with $k=7$? 4**) Is there a Moore graph with $k=5$? 5) Show that there is no Moore graph for other $k$'s. Send a solution

Problem 21. * Consider a 50-sided regular polygon. Dr. Faust is standing in one of its vertices. He has three possibilities: 1) to go to a diametrically opposite vertex free of charge; 2) to go to a counterclockwise neighboring vertex by paying \$1.05 to Mephistopheles; 3) to go to a clockwise neighboring vertex and receiving \$1.05 from Mephistopheles. It is known that Dr. Faust has been at each vertex at least once. Show that on some part of the path someone paid to the other at least \$25. Send a solution