Задача 7.

Найдите ошибку в следующих доказательствах. а) Докажем, что $n>n+1$. Действительно, пусть это утверждение верно для $n$, то есть $n>n+1$. Прибавив к обеим частям равенства единицу, мы получаем, что $(n+1)>(n+1)+1$, то есть верно утверждение для $n+1$. б) Докажем, что в произвольном стаде из $N$ коров все коровы одного цвета. База индукции. В любом стаде из одной коровы все коровы, очевидно, одного цвета. Шаг индукции. Предположим, что в любом стаде из $N$ коров все коровы одного цвета. Докажем, что в любом стаде из $N+1$ коровы все коровы одного цвета. Рассмотрим произвольное стадо из $N+1$ коровы. Возьмем в нем произвольную корову А. Оставшиеся $N$ коров одного цвета. Теперь возьмем другую корову B. Оставшиеся $N$ коров также одного цвета. В частности, А одного цвета со всеми коровами, кроме А и В, и В одного (того же!) цвета со всеми коровами, кроме А и В (см. рисунок). Значит, А, В, и вообще все коровы в стаде одного цвета. 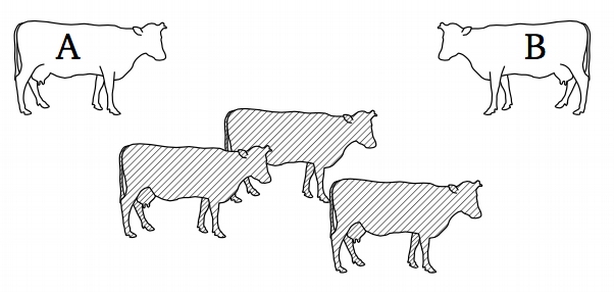в) В стране несколько городов, некоторые пары которых соединены дорогами, причем каждый город соединен хотя бы с одним другим. Докажем, что из любого города можно проехать в любой другой по дорогам. Будем доказывать индукцией по числу городов. База индукции для стран, состоящих из одного города, очевидна. Докажем шаг индукции. Возьмем какую-нибудь страну из $n$ городов и добавим к ней еще один город. Между старыми городами можно проехать по старым дорогам, так что достаточно доказать, что из нового города можно проехать в любой из старых. По условию задачи из этого города ведет дорога в один из старых городов. Следовательно, из него можно доехать в один из старых городов, а оттуда уже добраться до любого другого. Итак, в новой стране тоже можно из любого города доехать до любого другого, и шаг индукции доказан.