∆ Definition 1. Let $X$ and $Y$ be sets. If for each $x\in X$ there is a unique corresponding $f(x)\in Y$, then $f$ is called a mapping or a map from $X$ to $Y$. If $f(x)=y$, then $y$ is called the image of $x$ and $x$ is called a preimage of $y$. Notation: $f: X \rightarrow Y$.

Problem 1. Consider a map from the set of special symbols on your keyboard to the set of numbers. What is the image of %? What is the preimage of 2? Send a solution

Problem 2. Which of the following pictures define a map? 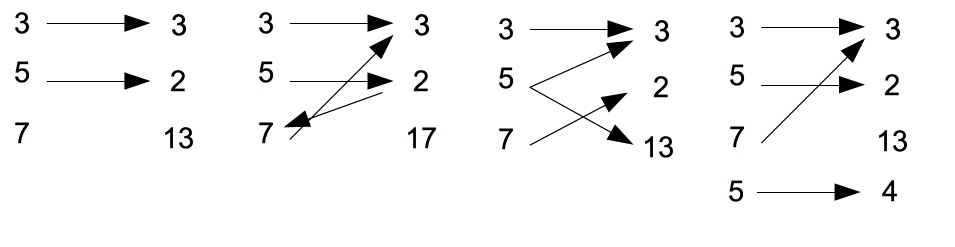Send a solution

Problem 3. How many maps are there from set $\{7,8,9\}$ to set $\{0,1\}$? Send a solution

Problem 4. Draw all the possible maps from set $\{7,8,9\}$ to set $\{0,1\}$? Send a solution

∆ Definition 2. Consider $f: X \rightarrow Y$, $y \in Y, A \subset X, B \subset Y$. The full preimage of $y$ is the set defined by {x ∈ X | f(x)= y}. Notation: $f^{−1}(y)$. The image of set $A \subset X$ is the set defined by {$f(x)$ | $x \in A$}. Notation: $f [A]$. The preimage of set $B \subset Y$ is the set defined by {$x \in X$ | $f(x) \in B$}. Notation: $f^{−1}[B]$.

Problem 5. Consider a map $f$: {0, 1, 3, 4} → {2, 5, 7, 18} defined on the picture below. Find $f$[{0, 3}], $f$[{1, 3, 4}], $f^{−1}$(2), $f^{−1}$[{2, 5}], $f^{−1}$[{5,18}].

a)

b)

c)

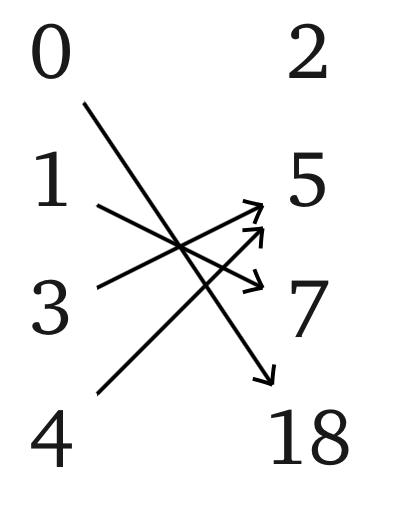
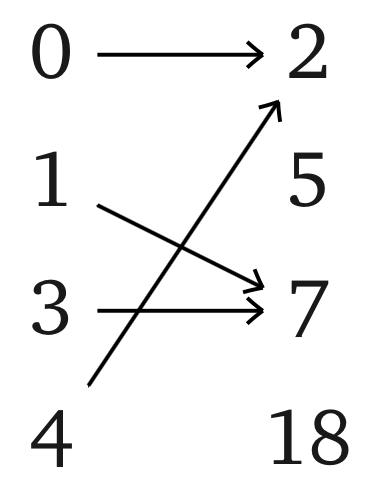
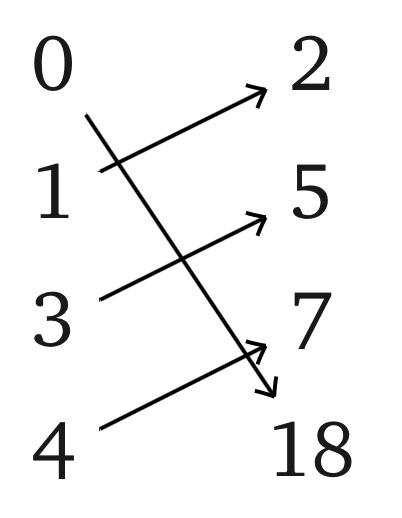
Problem 6. Consider $f\colon X\rightarrow Y$, $A_1, A_2\subset X$, $B_1, B_2\subset Y$. Is the following always true? a) $f[X]=Y$; b) $f^{-1}[Y]=X$; c) $f[A_1\cup A_2]=f[A_1]\cup f[A_2]$; d) $f[A_1\cap A_2] = f[A_1]\cap f[A_2]$; e) $f^{-1}[B_1\cup B_2] = f^{-1}[B_1]\cup f^{-1}[B_2]$; f) $f^{-1}[B_1\cap B_2] = f^{-1}[B_1]\cap f^{-1}[B_2]$; g) $f[A_1]\subset f[A_2] \Rightarrow A_1\subset A_2$; h) $f^{-1} [B_1] \subset f^{-1}[B_2]\Rightarrow B_1\subset B_2$. Send a solution

∆ Definition 3. Let $f: X \rightarrow Y$ and $g: Y \rightarrow Z$ be maps. The composite map is a map that for each element $x\in X$ puts into correspondance element $g(f(x))\in Z$. Notation: $g$ ◦ $f$. I.e. The composite map $g$ ◦ $f$ is defined by applying map $g$ to the result of applying map $f$ to $x$.

Problem 7. Show that for any maps $f : X \rightarrow Y, g: Y \rightarrow Z$ and $h: Z \rightarrow W$ the following is true $h$◦($g$◦$f$)=($h$◦$g$)◦$f$ (i.e. we can omit the parentheses in expression $h$◦$g$◦$f$). Send a solution

Problem 8. Consider the following maps $f$: {1,2,3,5}$\rightarrow${0,1,2}, $g$:{0,1,2}$\rightarrow${3,7,37,137}, $h$: {3, 7, 37, 137} $\rightarrow$ {1, 2, 3, 5} defined by the picture below.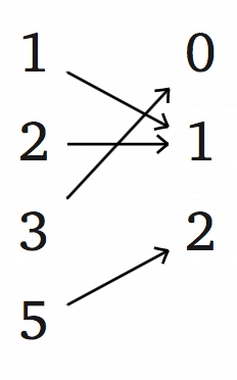

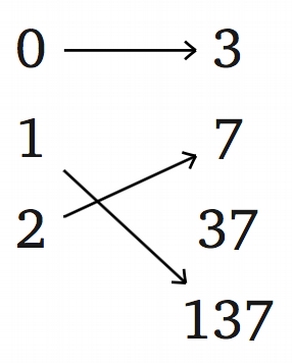
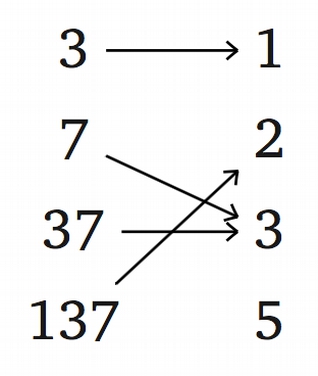
$f:$

$g:$

$h:$

∆ Definition 4. A map $f\colon X\rightarrow Y$ is called bijective if for each $y\in Y$ there is unique $x\in X$ such that $f(x)=y$.

Problem 9. Which of the following maps are bijective and which are not? 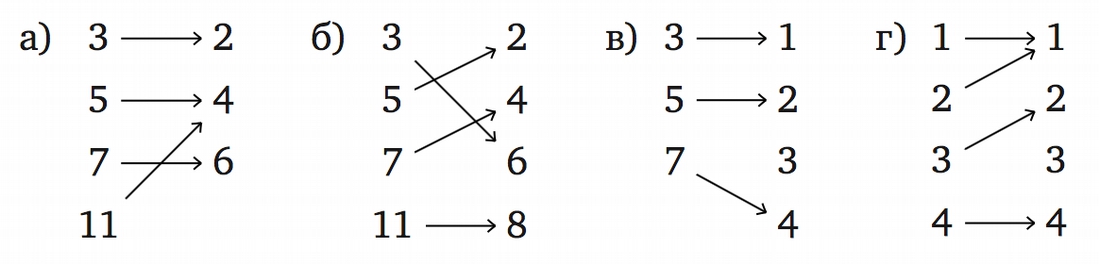Send a solution

Problem 10. Draw all the bijective maps a) from $\{1,2\}$ to $\{3,4,5,6\}$; b) from $\{1,2,3\}$ to $\{4,5,6\}$. Send a solution

Problem 11. Consider $f\colon X\rightarrow Y$, $g\colon Y\rightarrow Z$. Is it true that if $f$ and $g$ are bijective, then $g\circ f$ is also bijective? Send a solution

∆ Definition 5. A map $f$ is called injective if it never maps distinct element to the same element, i.e. from $f(x)=f(x')$ follows that $x=x'$. A map $f\colon X\to Y$ is called surjective if each element $y\in Y$ has at least one preimage, i.e. $f^{-1}(y)\ne\emptyset$ for any $y\in Y$.

Problem 12. Show that the following properties of a map $f \mkern-2mu\colon\mkern-2mu X\to Y$ are equivalent 1) $f$ is bijective; 2) $f$ is surjective and injective; 3) $f$ has an inverse, i.e. there is a map $g\colon Y\to X$ such that $g\circ f=\mathrm{Id}_X$, $f\circ g=\mathrm{Id}_Y$, where $\mathrm{Id}_M\colon M\to M$, $m\mapsto m$ is the identity map on a set $M$. Send a solution

Problem 13. Find all pairs of sets among the given below such that the sets in the pair are bijective: a) the set of natural numbers; b) the set of even natural numbers; c) the set of natural numbers except number $3$; d) the set of integer numbers. Send a solution