∆ Definition 1. Permutation of $n$ elements is a bijection from $\{1,2,...,n\}$ to itself. We denote by  $\left( \begin{smallmatrix} i_1&i_2&...&i_n \\ j_1&j_2&...&j_n \end{smallmatrix} \right)$, where $i_1,\,i_2,... ,\,i_n$  are different elements of the set  $\{1,2,... ,n\}$ and $j_1,\,j_2,... ,\,j_n$  are different elements of the set $\{1,2,... ,n\}$, permutation $a$ such that $a(i_k)=j_k$ for all $k\in \{1,2,... ,n\}$. We can graph a permutation in the following way. On a plane, draw elements of the set $\{1, 2, ..., n\}$, then for each element $i$ graph an arrow from $i$ to $a(i)$. The resulting graph is called the graph of the permutation. The set of permutations of $n$ elements is denoted by $S_n$.

Problem 1. Which of the following are permutations? $ a)\left( \begin{smallmatrix} 1 \\ 1 \end{smallmatrix} \right); b)\left( \begin{smallmatrix} 1&2&3 \\ 1&2&3 \end{smallmatrix} \right) ; c)\left( \begin{smallmatrix} 2 \\ 2 \end{smallmatrix} \right) ;\\ d) \left( \begin{smallmatrix} 1&2&3 \\ 2&3&4 \end{smallmatrix} \right) ; e) \left( \begin{smallmatrix} 1&2&3 \\ 3&3&3 \end{smallmatrix} \right) ;\\ f) \left( \begin{smallmatrix} 5&1&4&6&3&2 \\ 1&6&4&2&5&3 \end{smallmatrix} \right);\\ g)\left( \begin{smallmatrix} 4&3&2&1 \\ 1&2&3&4 \end{smallmatrix} \right) ; h)\left( \begin{smallmatrix} 5&3&2&1 \\ 5&3&2&1 \end{smallmatrix} \right) ;\\ i)\left( \begin{smallmatrix} 1&3&2&7 \\ 7&2&3&1 \end{smallmatrix} \right) ; j)\left( \begin{smallmatrix} 1&2&3 \\ 1&1&2 \end{smallmatrix} \right). $ Send a solution

Problem 2. Write out and graph all the elements of the sets $S_1$, $S_2$ and $S_3$. Send a solution

Problem 3. Which of the following graphs are the graphs of permutations? 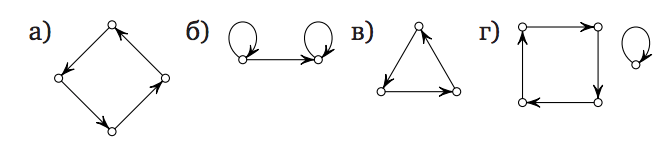Send a solution

Problem 4. 1) How many elements are in $S_n$? 2) In how many ways can a permutation of $n$ elements be described? Send a solution

∆ Definition 2. The product of permutations $a,b\in S_n$ is the permutation $a\circ b$. Notation: $ab$.

Problem 5. Find the following products: 1) $\left( \begin{smallmatrix} 1&2&3 \\ 3&1&2 \end{smallmatrix} \right)\! \left( \begin{smallmatrix}3&1&2 \\ 1&2&3\end{smallmatrix} \right)$; 2) $\left( \begin{smallmatrix}1&2&3&4 \\ 4&3&2&1\end{smallmatrix} \right)\! \left( \begin{smallmatrix}1&2&3&4 \\ 2&1&4&3\end{smallmatrix} \right)$; 3) $\left( \begin{smallmatrix}1&2&4&5&3&6 \\ 1&2&3&4&5&6\end{smallmatrix} \right)\! \left( \begin{smallmatrix}6&4&2&3&5&1 \\ 1&2&3&4&5&6\end{smallmatrix} \right)$; 4) $\left( \begin{smallmatrix}1&2&3&4&5 \\ 2&4&5&3&1\end{smallmatrix} \right)\! \left( \begin{smallmatrix}1&2&3&4&5 \\ 3&5&1&2&4\end{smallmatrix} \right)$; 5) $\left( \begin{smallmatrix}1&2&3&4&5&6 \\ 5&6&1&4&2&3\end{smallmatrix} \right)\! \left( \begin{smallmatrix}1&2&3&4&5&6 \\ 3&4&5&2&6&1\end{smallmatrix} \right)$ Send a solution

Problem 6. Is it true that for any permutations $a,b \in S_n$, we have $ab=ba$? Send a solution

∆ Definition 3. Permutation  $e=\left( \begin{smallmatrix}1&2&...&n \\ 1&2&...&n\end{smallmatrix} \right) $ is called the identity permutation.

Problem 7. Show that the following are true: 1) For any permutation $a\in S_n$ we have $ae=ea=a$. 2) For any permutations $a,b,c\in S_n$ we have $(ab)c=a(bc)$. 3) For any permutation $a\in S_n$ there is a unique permutatioin $b\in S_n$ such that $ab=ba=e$. Send a solution

∆ Definition 4. Let $1\leqslant i,j\leqslant n$, $i\ne j$. Permutation $a$ such that $a(i)=j$, $a(j)=i$, $a(k)=k$ for $k\ne i,j$ is called transposition. Notation: $(i,j)$.

∆ Definition 5. Let $i_1$, $i_2$, ..., $i_k$ be different elements of the set $\{1, 2, ..., n\}$. Permutation $a$ such that $a(i_j)=i_{j+1}$, $a(i_k)=i_1$ for any $j\in \{1, 2, ..., k - 1\}$, and $a(s)=s$ for any $s\notin \{i_1, i_2, ..., i_k\}$, is called a cycle of length $k$. Notation: $(i_1, i_2, ..., i_k)$. The set $\{i_1, ..., i_k\}$ is called the carrier of the cycle, and $k$ is called the length of the cycle.

Problem 8. 1) Which permutations from Problem 1 and Problem 2 are cycles and which are transpositions? 2) How many cycles of length $57$ are there in the set $S_{57}$? 3) How many cycles and how many transpositions are there in $S_{5}$? 4) When the product of two transpositions is a cycle? 5*) When the product of two cycles is a cycle? Send a solution

∆ Definition 6. Cycles with disjoint carriers are called independent.

Problem 9. *1) Show that any permutation can be written as a product of independent cycles. 2) Show that any permutation can be written as a product of transpositions. 3) Show that any permutation from $S_n$ can be written as a product of at most $(n-1)$ transpositions. 4) Is it true that any permutation from $S_n$ can be written as a product of independent transpositions? Send a solution