Notation. Below, $m$, $n$ and $k$ are natural numbers (positive integers).

Axiom. Any non-empty subset of the set of natural numbers has the minimal element, i.e. the element that is smaller than any other element in the subset.

Problem 1. a) Is the above axiom true if instead of the set of natural numbers we consider the set of integer numbers? b) Is the above axiom true if instead of the minimal element we consider the maximal element? Send a solution

Problem 2. On the Dream island, all the countries have triangular shapes. If two countries have a common boundary, then the boundary is the whole edge of a triangle. Show that the countries can be colored in such a way, that countries with a common boundary will be different colors. Send a solution

Mathematical induction. Suppose we have a set of statements $A_1, A_2, \dots, A_k, \ldots$, where 1) (the base case) the first statement is true; 2) (the step case) if $A_n$ is true, then $A_{n+1}$ is true. Then $A_k$ is true for any $k=1,2,\dots$. (Sometimes this statement is used as an axiom.)

Problem 3. Proof the above statement. Send a solution

Problem 4. On the Dream island, any two cities are connected by a direct highway or by a direct railway. Show that either from any city to any other we can get by car, or from any city to any other city we can get by train. Send a solution

Problem 5. Suppose we have $n$ lines that divide a plane into parts. Show that the parts can be colored in such a way that the neighboring parts (the ones that have an interval or a ray in common) will be different colors. Send a solution

Problem 6. Using induction, show the following: a) $1+\ldots+n=\frac{n(n+1)}2$; b) $1+\ldots+n^2=\frac{n(n+1)(2n+1)}6$; c) $1+\ldots+n^3=\frac{n^2(n+1)^2}4$. Send a solution

Problem 7. Find mistakes in the following proofs: a) A proof of $n>n+1$. Let this statement be true for $n$, i.e. $n>n+1$. By adding $1$ to the both sides of the inequality, we get $(n+1)>(n+1)+1$. Thus, the inequality is true for $n+1$. b) A proof that in a herd of $N$ cows all the cows have the same color. The induction base. In a herd of one cow, all the cows have the same color, obviously. The induction step. Suppose that in any herd of $N$ cows all the cows have the same color. Now we show that in any herd of $N+1$ cows all the cows have the same color. Consider a herd of $N+1$ cows. Choose a cow and call it A. The remaining $N$ cows have the same color. Choose another cow from the herd of $N+1$ and call it B. The remaining $N$ cows have the same color. In particular, A has identical color as the other cows, except B. And B has the same identical color as the other cows, except A, see the picture below. Thus, A, B and all the other cows have identical color. 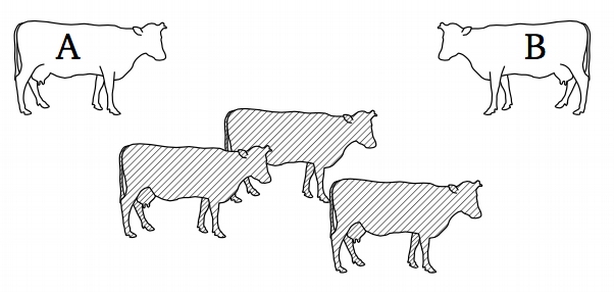c) There are several cities in a country. Some pairs of cities are connected by roads and any city is connected with at least one other. We show that we can drive from any city to any other. Apply mathematical induction using the number of cities. The induction base is a country with only one city. Now we proof the induction step. Consider a country with $n$ cities and add one new city to it. We can drive between the old $n$ cities, it remains to show that from the new city we can drive to any old city. Given that any city connected with at least one other, the new city is connected with at least one old. So, we can drive to the old city and from there drive to any other city. Thus, we proved the induction step. Send a solution

Problem 8. Lines are said to be in general position if none of the pairs of lines are parallel and no three lines intersect in a single point. Into how many parts $n$ lines in general position divide a plane? Send a solution

Problem 9. Show that: a) $2^{5n+3}+5^n\cdot 3^{n+2}$ делится на 17; b) $n^{2m-1}+1$ делится на $n+1$; c*) $2^{3^n}+1$ делится на $3^{n+1}$. Send a solution

Problem 10. (Bernoulli's inequality) Show that if $a>-1$, then $$(1+a)^n\ge 1+na\text{.}$$ Send a solution

Problem 11. Show that a) $2^n>n$;  b) $2^n>n^2$ for $n>4$;  c) $n!>2^n$ for $n>3$; d) there is $k$ such that $2^n>n^{2004}$ for all $n>k$. Send a solution

Problem 12. The vertices of a convex polygon are colored in three colors such that the neighboring vertices are different colors. Show that the polygon can be partitioned by diagonals into triangles in such a way that the vertices of each triangle are three different colors. Send a solution

Complete (strong) induction. Suppose we have a set of statements $A_1, A_2, \ldots, A_k, \ldots$, where 1) (the base case) the first statement is true; 2) (the step case) if $A_1, A_2, \ldots, A_n$ are all true, then $A_{n+1}$ is true. Then $A_k$ is true for any $k=1,2,\dots$.

Problem 13. * Prove the above statement. Send a solution

Problem 14. Show that if $a+\smash{\frac{1}{a}}$ is integer, then $a^k+\smash{\frac{1}{a^k}}$ is integer for any $k$. Send a solution

Problem 15. * In a group of students, each chatterbox is a pal of at least one mute. A mute is silent if there is odd number of his mute friends in the same classroom. Show that a teacher can let at most half of the students in a class go so that all the mutes become silent. Send a solution

Problem 16. * (Sylvester's Line Problem) Show that it is not possible to arrange a finite number of points so that a line through every two of them passes through a third unless they are all on a single line. Send a solution

Problem 17. * Show that $n^{n+1}>(n+1)^n$ for $n>2$. Send a solution