Задача 1. В турнире по олимпийской системе участвовали $n$ команд. Сколько всего было сыграно матчей? Отправить решение

Задача 2. Докажите, что граф с $n$ вершинами, степень каждой из которых не менее $\frac{n-1}{2}$, связен. Отправить решение

Задача 3. В связном графе все вершины имеют степень 100. Докажите, что после удаления любого из рёбер он остаётся связным. Отправить решение

Задача 4. Докажите, что в любом связном графе есть подграф, являющийся деревом и содержащий все вершины (максимальное поддерево). Отправить решение

Задача 5. Докажите, что из любого связного графа можно выкинуть вершину и выходящие из неё рёбра так, чтобы он остался связным. Отправить решение

Задача 6. * В кубической коробке $n\times n\times n$ лежали $n^3$ единичных кубиков. Кубики высыпали, каждый просверлили по диагонали, затем все плотно нанизали на нить и связали в кольцо (соединили вершину первого кубика с вершиной последнего). При каких n получившееся "ожерелье" можно убрать обратно в коробку? Отправить решение

Задача 7. * Все 28 Петиных одноклассников имеют по различному числу друзей в этом классе. Сколько из них дружат с Петей? А если одноклассников $n$? Отправить решение

Задача 8. * (Теорема Кэли) В графе с $n$ вершинами каждая вершина соединена с каждой ребром (такой граф называется полным). Докажите, что существует ровно $n^{n-2}$ способов выкинуть несколько рёбер так, чтобы оставшийся граф являлся деревом. Отправить решение

∆ Определение 1. Ориентированным графом называется граф, на рёбрах которого поставлены стрелки. Его рёбра называются дугами. Более формально, ориентированный граф — это пара $\Gamma=(V, E)$ из конечного множества вершин $V$ и множества дуг $E$, элементами которого являются упорядоченные пары вершин графа $\Gamma$. Заметим, что у нас в ориентированном графе разрешаются дуги из вершины в себя саму (петли), несколько дуг из одной вершины в другую (кратные дуги), "встречные" дуги (из $A$ в $B$ и из $B$ в $A$). То, что раньше называлось графом, мы теперь будем называть неориентированным графом.

Задача 9. Дайте (формальные!) определения пути и цикла в ориентированном графе. Отправить решение

∆ Определение 2. Ориентированный граф называется сильно связным, если для любых двух его вершин существует путь как из первой во вторую, так и из второй в первую.

Задача 10. Какие из следующих графов сильно связны? 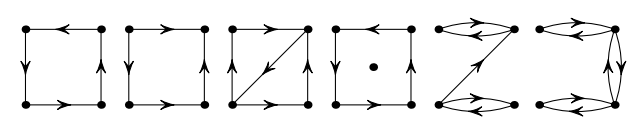Отправить решение

∆ Определение 3. Ориентированный граф называется связным, если он окажется связным неориентированным графом после того, как мы сотрём стрелки с его дуг.

Задача 11. 1) Приведите пример связного, но не сильно связного ориентированного графа. 2) Приведите пример связного ориентированного графа, в котором для некоторых двух вершин $A$ и $B$ нет пути ни из $A$ в $B$, ни из $B$ в $A$. Отправить решение

Задача 12. Докажите, что на рёбрах связного неориентированного графа можно так расставить стрелки, чтобы из одной из вершин существовали пути во все остальные. Отправить решение

Задача 13. Можно ли так расставить на рёбрах полного неориентированного графа стрелки, чтобы в полученном ориентированном графе не было циклов? Отправить решение

Задача 14. В полном неориентированном графе на рёбрах как-то расставили стрелки. Докажите, что найдётся вершина, из которой существуют пути во все остальные. Отправить решение

Задача 15. * (Задача 18* из первого листка про графы) В полном неориентированном графе на рёбрах как-то расставили стрелки. Докажите, что полученный граф гамильтонов. Отправить решение

Задача 16. * В полном неориентированном графе с не менее чем тремя вершинами на рёбрах как-то расставили стрелки. Докажите, что можно заменить не более одной дуги на противоположную так, чтобы полученный граф стал сильно связным. Отправить решение

∆ Определение 4. Количество дуг, входящих в вершину, называется входной полустепенью (или полустепенью захода) этой вершины. Количество выходящих дуг называется выходной полустепенью (или полустепенью исхода).

Задача 17. Найдите входные и выходные полустепени каждой вершины для всех графов из задачи 10. Отправить решение

Задача 18. Что можно сказать о сумме всех входных полустепеней и сумме всех выходных полустепеней одного и того же ориентированного графа? Отправить решение

Задача 19. Сформулируйте и докажите критерий эйлеровости ориентированного графа. Отправить решение

Задача 20. (Цикл де Брюина) Для того, чтобы открыть кодовый замок (с кнопками от 0 до 9), необходимо набрать код из четырёх цифр, причём не важно, что было нажато до набора правильного кода. За какое наименьшее количество нажатий его можно гарантированно открыть? Отправить решение

Задача 21. 20 школьников решали 20 задач. Каждый решил ровно две задачи, и каждую задачу решили ровно двое. Доказать, что можно устроить разбор задач так, чтобы каждый рассказал одну решённую им задачу. Отправить решение

∆ Определение 5. Граф называется двудольным, если его вершины можно разбить на две группы (называемые долями) так, чтобы все рёбра (или дуги) были между различными долями. Паросочетанием называется такой набор рёбер графа, что каждая вершина графа является концом не более одного ребра из набора. Паросочетание называется совершенным, если каждая вершина является концом ровно одного ребра паросочетания. Раскраска вершин графа называется правильной, если никакие две вершины одного цвета на соединены ребром. Граф называется $k$-дольным, если правильная раскраска его вершин возможна $k$ цветами и не менее.

Задача 22. Какие графы из задач 1, 2, 3 первого листка про графы являются двудольными? А сколько-дольными являются остальные? Отправить решение

Задача 23. Равносильна ли двудольность неориентированного графа отсутствию циклов нечётной длины? Отправить решение

Задача 24. Любое ли дерево двудольно? Отправить решение

Задача 25. * (теорема Холла) В некой компании $n$ юношей. При каждом $k=1$, $2$, ..., $n$ для любых $k$ юношей в этой компании найдется не менее $k$ девушек, знакомых хотя бы с одним из рассматриваемых $k$ юношей. Можно ли просватать всех юношей за знакомых девушек? Является ли это условие необходимым? Иными словами, верно ли, что в двудольном неориентированном графе (с $n$ вершинами в первой доле) существует паросочетание размера $n$ тогда и только тогда, когда для каждого набора из $k$ вершин первой доли с ними соединены хотя бы $k$ вершин второй доли? Отправить решение

Задача 26. * (Обобщение задачи 21) Докажите, что в любом регулярном двудольном неориентированном графе есть совершенное паросочетание. Отправить решение

Задача 27. * Верно ли, что при любой правильной раскраске $k$-дольного неориентированного графа в $k$ цветов найдётся путь из $k$ разноцветных вершин? Отправить решение

∆ Определение 6. Граф называется планарным, если его можно нарисовать на плоскости, изобразив вершины точками, а рёбра (или дуги) — непересекающимися кривыми. Граф, который нарисован на плоскости указанным выше образом, называется плоским. Части, на которые плоский граф делит плоскость (включая внешнюю часть) называются его гранями.

Задача 28. Какие графы из задач 1, 2, 3(1) первого листка про графы являются планарными? Отправить решение

Задача 29. (Формула Эйлера) Пусть в неориентированном плоском связном графе $В$ вершин, $Р$ рёбер и $Г$ граней. Тогда $В+Г-Р=2$. Отправить решение

Задача 30. Чему равно $В+Г-Р$ для несвязного неориентированного плоского графа? Отправить решение

Задача 31. Пусть $В$, $Р$ и $Г$ — количества вершин, рёбер и граней многогранника соответственно. Чему равно $В+Г-Р$? Отправить решение

Задача 32. 1) Докажите, что в плоском неориентированном графе $2Р\geqslant 3Г$. 2) Докажите, что в плоском двудольном неориентированном графе $Р\geqslant 2Г$. Отправить решение

Задача 33. Докажите, что следующие графы не планарны: 1) Полный неориентированный граф с 5 вершинами. Этот граф обозначается $K_5$. 2) Двудольный неориентированный граф с 3 вершинами в первой доле и 3 вершинами во второй доле, причём каждая вершина первой доли соединена с каждой вершиной второй (такой граф называется полным двудольным). Этот граф обозначается $K_{3,3}$. 3) Произвольный неориентированный граф, у которого степени всех вершин не меньше шести. Отправить решение

∆ Определение 7. Подграфом данного графа называется граф, который получается из данного выкидыванием некоторых вершин и рёбер (дуг). Два неориентированных графа называются гомеоморфными, если один можно получить из другого следующими операциями: взять ребро и добавить посередине этого ребра вершину; взять вершину степени 2 и заменить её и выходящие из неё рёбра на одно ребро (заметим, что эти две операции взаимно обратны).

Задача 34. * (Теорема Понтрягина-Куратовского) Докажите, что неориентированный граф планарен тогда и только тогда, когда у него нет подграфа, гомеоморфного $K_5$ или $K_{3,3}$. Отправить решение