Комбинаторика 2. Бином Ньютона
∆ Определение 1.
Треугольником Паскаля называется треугольная таблица, составленная из чисел по следующему правилу: строка с номером $n$ состоит из $n$ чисел, первое и последнее числа каждой строки равны единице, а каждое из остальных чисел равно сумме двух ближайших к нему чисел предыдущей строки. Число, стоящее на $(k+1)$-м месте $(n+1)$-й строки обозначается $\binom{n}{k}$. 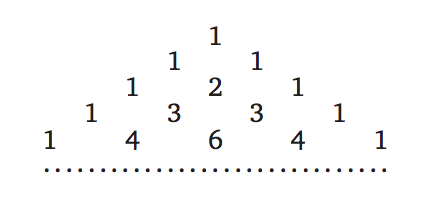
Задача 1. Выпишите первые 11 строк треугольника Паскаля. Отправить решение
Задача 2. Докажите, что $\binom{n}{k}=\binom{n}{n-k}$. Отправить решение
Задача 3. Докажите, что число способов пройти из левого нижнего угла прямоугольника $m\times n$ в правый верхний, идя только вверх или вправо, равно $\binom{n+m}{m}$. Отправить решение
Задача 4. * В каких строках треугольника Паскаля все числа — нечётные? Отправить решение
∆ Определение 2. Числом сочетаний из $n$ по $m$ называется количество $m$-элементных подмножеств множества из $n$ элементов. Обозначение: $C_n^m$.
Задача 5. Найти 1) $C_{100}^1$, 2) $C_4^2$, 3) $C_5^2$, 4) $C_6^4$. Отправить решение
Задача 6. Докажите что 1) $C_n^k=C_n^{n-k}$ 2) $C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$. Отправить решение
Задача 7. Докажите, что $\binom{n}{k}=C_n^k$. Отправить решение
Задача 8. Раскройте скобки в выражении 1) $(a+b)^3$ 2) $(a+b)^4$ 3) $(2a+3b)^4$. Отправить решение
Задача 9. (Бином Ньютона) 1) раскройте скобки в выражениях $(a+b)$, $(a+b)^2$, $(a+b)^3$, $(a+b)^4$ и выпишите результаты друг под другом. Заметьте, что коэффициенты образуют треугольник Паскаля. 2) Докажите, что \begin{equation*} (a+b)^n = \binom{n}{0}a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b^2 + ... + \binom{n}{n}b^n. \end{equation*} Отправить решение
Задача 10. Докажите, что 1) $\binom{n}{0}+\binom{n}{1}+...+\binom{n}{n}=2^n;$ 2) $\binom{n}{0}-\binom{n}{1}+...+(-1)^n\binom{n}{n}=0$. Отправить решение
Задача 11. Докажите, что $\binom{n}{k}=\frac{n!}{k!(n-k)!}$. Отправить решение
Задача 12. Докажите, что \begin{equation*} \begin{array}{ll} 1) \binom{n}{0}^2+\binom{n}{1}^2+...+\binom{n}{n}^2=\binom{2n}{n};\\ 2) \binom{n}{0}+\binom{n+1}{1}+...+\binom{n+k-1}{k-1}+\binom{n+k}{k} = \binom{n+k+1}{k}; \\ 3) \binom{n}{1}+2\binom{n}{2}+...+n\binom{n}{n}= n2^{n-1};\\ 4) \binom{n}{k}\cdot\binom{n-k}{m-k}=\binom{m}{k}\cdot\binom{n}{m}. \end{array} \end{equation*} Отправить решение
Задача 13. Каких подмножеств в множестве из 16 элементов больше: состоящих из более чем 8 элементов; из менее чем 8 элементов; из ровно 8 элементов? Отправить решение
Задача 14. Найдите число таких последовательностей длины 16 из нулей и единиц, в которых не менее чем три единицы. Отправить решение
Задача 15. Решите указанные преподавателем задачи из листка Комбинаторика 1 для произвольных $n$ и $k$. Отправить решение
Задача 16. * Сколькими способами можно выбрать неотрицательные целые числа $x_1,x_2,...,x_m$ такие, что $x_1+x_2+...+x_m=n$? Отправить решение