∆ Определение 1. Если каждому элементу $x$ множества $X$ поставлен в соответствие ровно один элемент $f(x)$ множества $Y$, то говорят, что задано отображение $f$ из множества $X$ в множество $Y$. При этом, если $f(x) = y$, то элемент $y$ называется образом элемента $x$ при отображении $f$, а элемент $x$ называется прообразом элемента $y$ при отображении $f$. Обозначение: $f: X \rightarrow Y$.

Задача 1. Рассмотрим отображение из множества латинских букв во множество кириллических, задаваемое компьютерной клавиатурой. Какая буква является образом буквы 'f'? Какая буква является прообразом буквы 'щ'? Отправить решение

Задача 2. Какие из следующих картинок задают отображения? 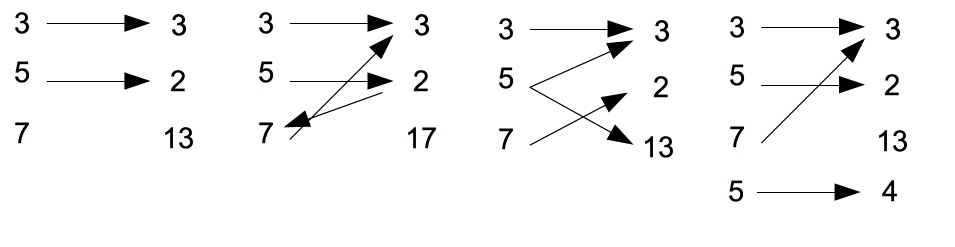Отправить решение

Задача 3. Сколько существует различных отображений из множества {7,8,9} во множество {0,1}? Отправить решение

Задача 4. Нарисуйте все возможные отображения из множества {7, 8, 9} в множество {0, 1}. Отправить решение

∆ Определение 2. Пусть $f: X \rightarrow Y$, $y \in Y, A \subset X, B \subset Y$. Полным прообразом элемента $y$ при отображении $f$ называется множество {x ∈ X | f(x)= y}. Обозначение: $f^{−1}(y)$. Образом множества $A \subset X$ при отображении $f$ называется множество {$f(x)$ | $x \in A$}. Обозначение: $f [A]$. Прообразом множества $B \subset Y$ называется множество {$x \in X$ | $f(x) \in B$}. Обозначение: $f^{−1}[B]$.

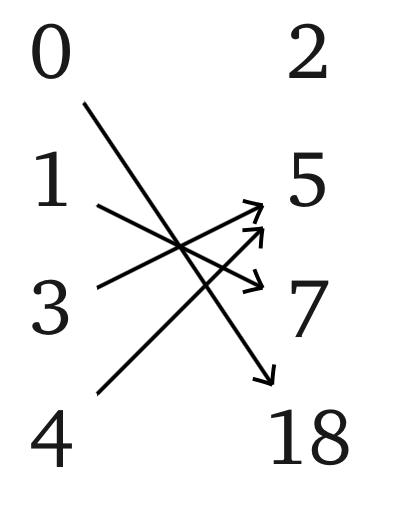
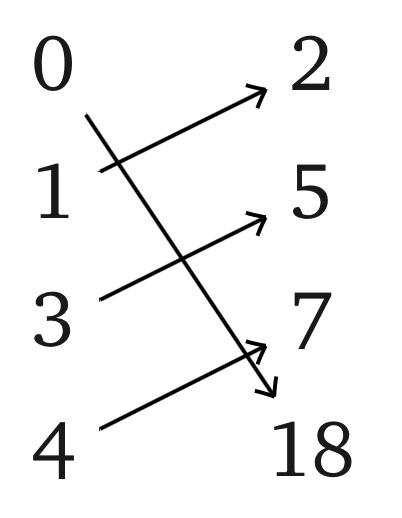
Задача 5. Для отображения $f$: {0, 1, 3, 4} → {2, 5, 7, 18}, заданного картинкой, найдите $f$[{0, 3}], $f$[{1, 3, 4}], $f^{−1}$(2), $f^{−1}$[{2, 5}], $f^{−1}$[{5,18}].

а)

б)

в)

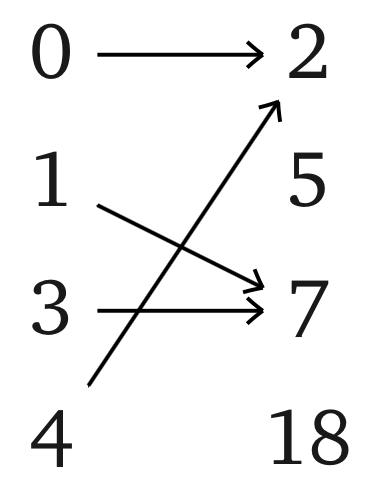
Задача 6. Пусть $f\colon X\rightarrow Y$, $A_1, A_2\subset X$, $B_1, B_2\subset Y$. Всегда ли верно, что а) $f[X]=Y$; б) $f^{-1}[Y]=X$; в) $f[A_1\cup A_2]=f[A_1]\cup f[A_2]$; г) $f[A_1\cap A_2] = f[A_1]\cap f[A_2]$; д) $f^{-1}[B_1\cup B_2] = f^{-1}[B_1]\cup f^{-1}[B_2]$; е) $f^{-1}[B_1\cap B_2] = f^{-1}[B_1]\cap f^{-1}[B_2]$; ж) $f[A_1]\subset f[A_2] \Rightarrow A_1\subset A_2$; з) $f^{-1} [B_1] \subset f^{-1}[B_2]\Rightarrow B_1\subset B_2$? Отправить решение

∆ Определение 3. Композицией отображений $f: X \rightarrow Y$ и $g: Y \rightarrow Z$ называется отображение, сопоставляющее элементу $x$ множества $X$ элемент $g(f(x))$ множества $Z$. Обозначение: $g$ ◦ $f$. (То есть композиция $g$ ◦ $f$ состоит в последовательном применении отображений $f$ и $g$.)

Задача 7. Докажите, что для произвольных отображений $f : X \rightarrow Y, g: Y \rightarrow Z$ и $h: Z \rightarrow W$ выполняется следующее: $h$◦($g$◦$f$)=($h$◦$g$)◦$f$ (то есть скобки в выражении $h$◦$g$◦$f$ можно не писать). Отправить решение

Задача 8. Пусть $f$: {1,2,3,5}$\rightarrow${0,1,2}, $g$:{0,1,2}$\rightarrow${3,7,37,137}, $h$: {3, 7, 37, 137} $\rightarrow$ {1, 2, 3, 5} — отображения, показанные на рисунке: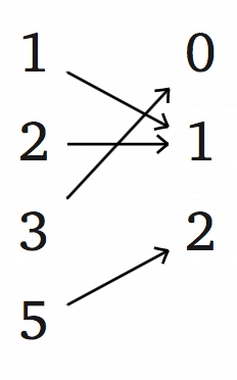

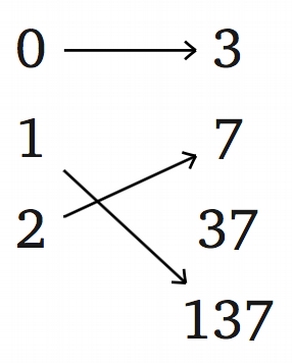
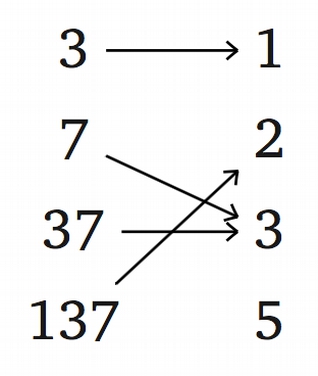
$f:$

$g:$

$h:$

∆ Определение 4. Отображение $f\colon X\rightarrow Y$ называется биективным, если для каждого $y\in Y$ найдется ровно один $x\in X$ такой, что $f(x)=y$.

Задача 9. Про каждое из отображений, изображенных на рисунке, выясните, является ли оно биективным: 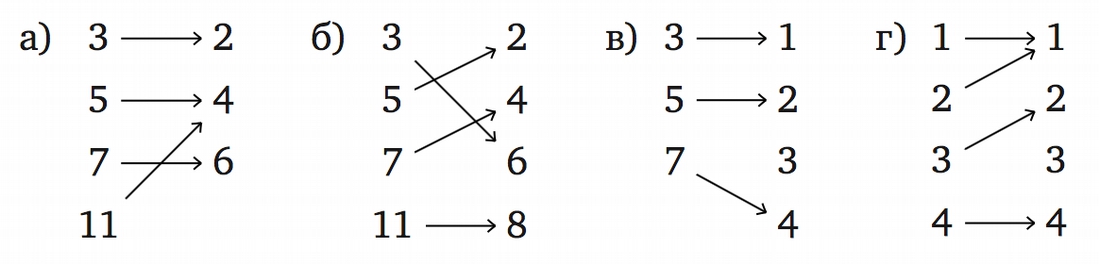Отправить решение

Задача 10. Нарисуйте все биективные отображения а) из множества $\{1,2\}$ в множество $\{3,4,5,6\}$; б) из множества $\{1,2,3\}$ в множество $\{4,5,6\}$. Отправить решение

Задача 11. Пусть $f\colon X\rightarrow Y$, $g\colon Y\rightarrow Z$. Верно ли, что если $f$ и $g$ биективны, то и $g\circ f$ биективно? Отправить решение

∆ Определение 5. Отображение $f$ называется инъективным, если оно разные элементы переводит в разные, т.е. если из $f(x)=f(x')$ следует, что $x=x'$. Отображение $f\colon X\to Y$ называется сюръективным, если каждый элемент $y\in Y$ имеет хотя бы один прообраз, т.е. $f^{-1}(y)\ne\emptyset$ для любого $y\in Y$.

Задача 12. Докажите, что следующие свойства отображения $f \mkern-2mu\colon\mkern-2mu X\to Y$ эквивалентны: 1) $f$ — биекция; 2) $f$ сюръективно и инъективно; 3) $f$ обратимо, то есть существует такое отображение $g\colon Y\to X$, что $g\mkern-1mu f=\mathrm{Id}_X$, $fg=\mathrm{Id}_Y$, где $\mathrm{Id}_M\colon M\to M$, $m\mapsto m$ — тождественное отображение. Отправить решение

Задача 13. Про каждые два из следующих множеств выясните, существует ли между ними биекция: а) множество натуральных чисел; б) множество четных натуральных чисел; в) множество натуральных чисел без числа 3; г) множество целых чисел. Отправить решение