∆ Определение 1. Подстановкой из $n$ элементов называется биективное отображение из множества $\{1,2,...,n\}$ в себя. Запись вида $\left( \begin{smallmatrix} i_1&i_2&...&i_n \\ j_1&j_2&...&j_n \end{smallmatrix} \right)$, где $i_1,\,i_2,... ,\,i_n$ — различные элементы множества $\{1,2,... ,n\}$ и $j_1,\,j_2,... ,\,j_n$ — различные элементы множества $\{1,2,... ,n\}$, обозначает подстановку $a$, для которой $a(i_k)=j_k$ при всех $k\in \{1,2,... ,n\}$. Множество подстановок из $n$ элементов обозначается $S_n$. Подстановку можно графически изобразить следующим образом. Изобразим на плоскости элементы множества $\{1, 2, ..., n\}$ и для каждого $i$ проведём стрелку из элемента $i$ в элемент $a(i)$. Полученное изображение называется графом подстановки.

Задача 1. Какие из следующих таблиц являются записями подстановок? $ a)\left( \begin{smallmatrix} 1 \\ 1 \end{smallmatrix} \right); b)\left( \begin{smallmatrix} 1&2&3 \\ 1&2&3 \end{smallmatrix} \right) ; c)\left( \begin{smallmatrix} 2 \\ 2 \end{smallmatrix} \right) ;\\ d) \left( \begin{smallmatrix} 1&2&3 \\ 2&3&4 \end{smallmatrix} \right) ; e) \left( \begin{smallmatrix} 1&2&3 \\ 3&3&3 \end{smallmatrix} \right) ;\\ f) \left( \begin{smallmatrix} 5&1&4&6&3&2 \\ 1&6&4&2&5&3 \end{smallmatrix} \right);\\ g)\left( \begin{smallmatrix} 4&3&2&1 \\ 1&2&3&4 \end{smallmatrix} \right) ; h)\left( \begin{smallmatrix} 5&3&2&1 \\ 5&3&2&1 \end{smallmatrix} \right) ;\\ i)\left( \begin{smallmatrix} 1&3&2&7 \\ 7&2&3&1 \end{smallmatrix} \right) ; j)\left( \begin{smallmatrix} 1&2&3 \\ 1&1&2 \end{smallmatrix} \right). $ Отправить решение

Задача 2. Выпишите и изобразите графически все элементы множеств $S_1$, $S_2$ и $S_3$. Отправить решение

Задача 3. Какие из следующих изображений являются графами подстановок? 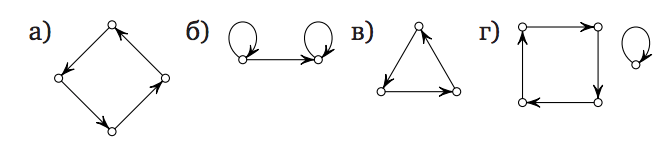Отправить решение

Задача 4. 1) Сколько элементов в множестве $S_n$? 2) Сколькими способами можно записать подстановку из $n$ элементов? Отправить решение

∆ Определение 2. Произведением подстановок $a,b\in S_n$ называется подстановка $a\circ b$. Обозначение: $ab$.

Задача 5. Найдите произведения: 1) $\left( \begin{smallmatrix} 1&2&3 \\ 3&1&2 \end{smallmatrix} \right)\! \left( \begin{smallmatrix}3&1&2 \\ 1&2&3\end{smallmatrix} \right)$; 2) $\left( \begin{smallmatrix}1&2&3&4 \\ 4&3&2&1\end{smallmatrix} \right)\! \left( \begin{smallmatrix}1&2&3&4 \\ 2&1&4&3\end{smallmatrix} \right)$; 3) $\left( \begin{smallmatrix}1&2&4&5&3&6 \\ 1&2&3&4&5&6\end{smallmatrix} \right)\! \left( \begin{smallmatrix}6&4&2&3&5&1 \\ 1&2&3&4&5&6\end{smallmatrix} \right)$; 4) $\left( \begin{smallmatrix}1&2&3&4&5 \\ 2&4&5&3&1\end{smallmatrix} \right)\! \left( \begin{smallmatrix}1&2&3&4&5 \\ 3&5&1&2&4\end{smallmatrix} \right)$; 5) $\left( \begin{smallmatrix}1&2&3&4&5&6 \\ 5&6&1&4&2&3\end{smallmatrix} \right)\! \left( \begin{smallmatrix}1&2&3&4&5&6 \\ 3&4&5&2&6&1\end{smallmatrix} \right)$ Отправить решение

Задача 6. Верно ли, что для любых подстановок $a,b\in S_n$ выполняется равенство $ab=ba$? Отправить решение

∆ Определение 3. Подстановка $e=\left( \begin{smallmatrix}1&2&...&n \\ 1&2&...&n\end{smallmatrix} \right) $ называется тождественной.

Задача 7. Докажите следующие утверждения: 1) Для любой подстановки $a\in S_n$ $ae=ea=a$. 2) Для любых подстановок $a,b,c\in S_n$ $(ab)c=a(bc)$. 3) Для любой подстановки $a\in S_n$ существует и при том единственная подстановка $b\in S_n$ такая, что $ab=ba=e$. Отправить решение

∆ Определение 4. Пусть $1\leqslant i,j\leqslant n$, $i\ne j$. Подстановка $a$ такая, что $a(i)=j$, $a(j)=i$, $a(k)=k$ при $k\ne i,j$ называется транспозицией. Обозначение: $(i,j)$.

∆ Определение 5. Пусть $i_1$, $i_2$, ..., $i_k$ — различные элементы множества $\{1, 2, ..., n\}$. Подстановка $a$, такая что для любого $j\in \{1, 2, ..., k - 1\}$ $a(i_j)=i_{j+1}$, $a(i_k)=i_1$ и $a(s)=s$ при $s\notin \{i_1, i_2, ..., i_k\}$, называется циклом длины $k$. Обозначение: $(i_1, i_2, ..., i_k)$. Множество $\{i_1, ..., i_k\}$ называется носителем цикла, а число $k$ — длиной цикла.

Задача 8. 1) Какие из подстановок задач 1 и 2 являются циклами, а какие — транспозициями? 2) Сколько циклов длины 57 в $S_{57}$? 3) Сколько циклов и сколько транспозиций в $S_{5}$? 4) При каких условиях произведение двух транспозиций является циклом? 5*) При каких условиях произведение двух циклов является циклом? Отправить решение

∆ Определение 6. Циклы с непересекающимися носителями называются независимыми.

Задача 9. * 1) Докажите, что любая подстановка представляется в виде произведения независимых циклов. 2) Докажите, что любая подстановка представляется в виде произведения транспозиций. 3) Докажите, что любая подстановка из $S_n$ представляется в виде произведения не более, чем $(n-1)$-й транспозиции. 4) Верно ли, что любая подстановка из $S_n$ представляется в виде произведения независимых транспозиций? Отправить решение