∆ Определение 1. Графом называется пара $\Gamma=(V, E)$ из конечного множества вершин $V$ и множества рёбер $E$, элементами которого являются (неупорядоченные) пары вершин графа $\Gamma$.

∆ Определение 2. Графы $\Gamma_1$ и $\Gamma_2$ называются изоморфными, если существует такая биекция $f\colon V(\Gamma_1)\to V(\Gamma_2)$, что вершины $A$ и $B$ графа $\Gamma_1$ соединены ребром тогда и только тогда, когда вершины $f(A)$ и $f(B)$ соединены ребром в графе $\Gamma_2$.

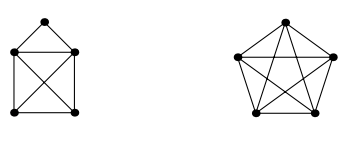
Задача 1. Какие из следующих графов изоморфны? (тут несколько графов) Отправить решение

Задача 2. Нарисуйте все неизоморфные друг другу графы с не более чем четырьмя вершинами. Отправить решение

Задача 3. 1) Нарисуйте граф, вершинами которого являются страны СНГ, а рёбрами соединены граничащие страны. 2) Нарисуйте граф, вершинами которого являются натуральные числа от $1$ до $15$, а рёбрами соединены числа, одно из которых делится на другое. Отправить решение

Задача 4. 1) Постройте граф с пятью вершинами, в котором нет ни трёх попарно соединённых, ни трёх попарно несоединённых вершин. 2) Докажите, что в каждой компании из шести человек найдутся либо три попарно знакомых, либо три попарно незнакомых человека. Отправить решение

Задача 5. Пусть в некоторой компании среди любых трёх человек найдутся два друга. Обязательно ли эту компанию можно разбить на две группы, так что всякие два человека из одной группы — друзья? Отправить решение

Задача 6. Найти наибольшее возможное количество рёбер в графе с $n$ вершинами, если известно, что среди произвольных 1) трёх, 2*) четырёх его вершин есть две, не соединённые ребром. Отправить решение

∆ Определение 3. Степенью вершины $A$ называется число выходящих из неё рёбер. Обозначение: $\deg A$.

Задача 7. Укажите степени всех вершин графов из задач 1, 2, 3 . Отправить решение

Задача 8. Докажите, что в графе с более чем одной вершиной есть две вершины одинаковой степени. Отправить решение

Задача 9. Докажите, что сумма степеней вершин произвольного графа равна удвоенному количеству его рёбер. Отправить решение

∆ Определение 4. Путём в графе называется конечная последовательность вершин (не обязательно различных), в которой всякие две соседние вершины соединены ребром. Путь называется проходящим по данному ребру, если это ребро соединяет некоторую пару соседних вершин пути. Циклом называется путь, в котором первая и последняя вершины совпадают. Длиной пути называется число рёбер, по которым проходит этот путь. В графе без кратных ребер (а в этом листке изучаются только такие графы) путь однозначно восстанавливается по последовательности своих вершин, поэтому обычно выписывают именно эту последовательность. Однако технически удобнее включать ребра в определение.

∆ Определение 5. Граф $\Gamma$ называется гамильтоновым, если в нём существует путь, содержащий каждую вершину ровно один раз.

Задача 10. Докажите, что графы додекаэдра и икосаэдра гамильтоновы. Отправить решение

∆ Определение 6. Граф называется связным, если для любых двух его вершин существует путь, начинающийся в первой из них и заканчивающийся во второй.

Задача 11. Какие из графов задач 1, 2, 3 связны? Отправить решение

Задача 12. Докажите, что если граф, число вершин которого больше $1$, связен, то степень любой его вершины положительна. Верно ли обратное? Отправить решение

∆ Определение 7. Связный граф называется деревом, если в нём не существует цикла, все рёбра которого различны.

Задача 13. Докажите, что в любом дереве есть вершина степени $1$. Отправить решение

Задача 14. Докажите, что в дереве число вершин на $1$ больше числа рёбер. Отправить решение

Задача 15. На рисунке изображена схема расположения мостов в городе Кёнигсберге XVIII века. Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно один раз? 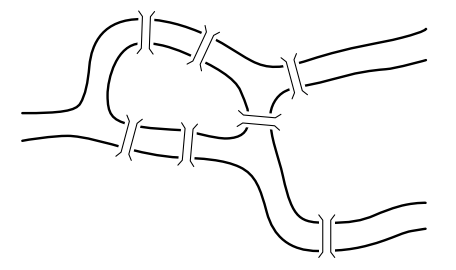Отправить решение

∆ Определение 8. Граф называется эйлеровым, если в нём существует цикл, проходящий по каждому ребру ровно один раз.

Задача 16. Доказать, что следующие графы эйлеровы: Отправить решение

Задача 17. Докажите, что граф эйлеров тогда и только тогда, когда он связен и степень каждой его вершины чётна. Отправить решение

Задача 18. * В турнире без ничьих участвовало $n$ команд. Каждая команда сыграла с каждой ровно по одному разу. Докажите, что можно так занумеровать команды числами $1,...,n$, что $(i+1)$-я команда выиграла у $i$-й (для произвольного $i=1,...,n-1$). Отправить решение

Задача 19. * (теорема Рамсея) 1) Докажите, что для произвольных натуральных $m,n$ существует натуральное $k$ такое, что в произвольном графе с $k$ вершинами найдётся либо $m$ попарно соединённых рёбрами вершин, либо $n$ попарно несоединённых. Наименьшее такое $k$ обозначается $R(m,n)$. 2) Найдите $R(3,4)$. Отправить решение

∆ Определение 9. Назовём расстоянием между вершинами связного графа наименьшую длину пути, соединяющего эти вершины. Диаметром графа называется наибольшее расстояние между его вершинами.

∆ Определение 10. Граф называется регулярным графом валентности $k$, если степень каждой его вершины равна $k$.

∆ Определение 11. Графом Мура называется регулярный граф валентности $k$ диаметра $\leqslant 2$, число вершин которого равно $k^2+1$.

Задача 20. * 1) Докажите, что в регулярном графе валентности $k$ и диаметра $2$ не может быть больше, чем $k^2+1$ вершина; 2) Приведите примеры графов Мура при $k=1, 2, 3$; 3) Существует ли граф Мура при $k=7$? 4**) Существует ли граф Мура при $k=57$? 5) Докажите, что ни при каких других значениях $k$ не существует графов Мура. Отправить решение

Задача 21. * Дан правильный $50$-угольник. В одной из его вершин стоит доктор Фауст. У него есть три возможности: 1) бесплатно перейти в диаметрально противоположную точку; 2) заплатив Мефистофелю 1 рубль 05 копеек, перейти на соседнюю вершину против часовой стрелки; 3) получив от Мефистофеля 1 рубль 05 копеек перейти на соседнюю вершину по часовой стрелке. Известно, что доктор Фауст везде побывал (хотя бы один раз). Докажите, что на каком-то отрезке пути кто-то кому-то заплатил не меньше $25$ рублей. Отправить решение